Kleine Wuerfelkunde - Basiswissenn#184; Entwurf eines Rollenspiel-Systems

Kleine Würfelkunde - Basiswissen¸ Entwurf eines Rollenspiel-Systems
von Xiang (Dirk Hennig)

Bezeichnung: Kleine Würfelkunde

Motivation: Basiswissen, Entwurf eines Rollenspiel-Systems

Gehört zum Kapitel: Grundregeln

Ein Beitrag von Xiang (Dirk Hennig)

Kaum ein Rollenspiel kommt ohne sie aus: Würfel. Mit ihnen wird bestimmt, ob eine Aktion erfolgreich ist, wo getroffen wird oder teilweise sogar der Charakter an sich ausgewürfelt. Dabei gibt es nicht nur eine ganze Menge an verschiedenen Würfeln - von denen hier nur auf die Klassiker W4, W6, W8, W10, W12 und W20 hingewiesen sein - sondern auch mindestens drei verschiedene Arten sie zu benutzen. Diese sollen im Folgenden ein wenig näher betrachtet werden.

1) Einzelne Würfel

Ein Würfel im mathematischen Sinn ist nur der W6. Im Rollenspiel aber werden damit beliebige gleichseitige Körper mit Zahlen drauf bezeichnet. Für solche Körper gilt, dass die Wahrscheinlichkeit mit der eine Seite (und damit die dort abgedruckte Zahl) oben liegt, für alle Seiten gleich ist. Der Wahrscheinlichkeitswert in Prozent berechnet sich dabei aus der Formel 100(Prozent) geteilt durch Seitenzahl. Bei einem W10 ist die Wahrscheinlichkeit für jede Seite also 10%, bei einem W20 sind es 5% usw. Grafisch ist das Ganze hier mal am Beispiel des W10 gezeigt:

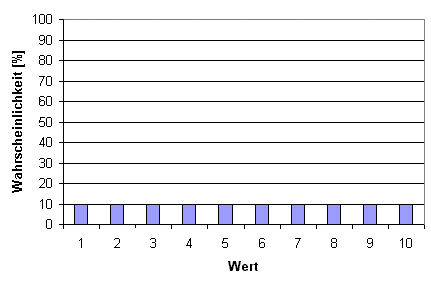
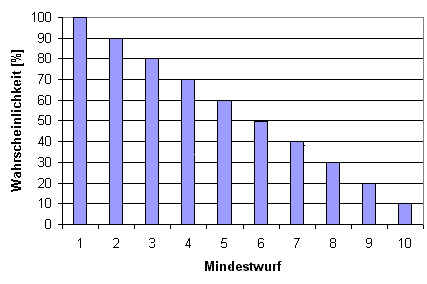
Häufig ist es aber nicht so sehr interessant, wie oft die einzelne Zahl fällt. Vielmehr geht es in einer Probe um einen Mindestwurf, der erreicht werden muss. Nun ist also die Frage, ob die gewürfelte Zahl größer oder gleich dem Mindestwurf ist. Hierbei addieren sich die Wahrscheinlichkeiten der Seiten, die diese Forderung erfüllen. Bei einem W10 ist die Wahrscheinlichkeit für das Erreichen eines Mindestwurfes 8 also 10% für die Seite 8 plus 10% für die Seite 9 plus 10% für die Seite 10, also insgesamt 30%. Die Grafik zeigt die Ergebnisse auch für andere Mindestwürfe.

Wenn es darum geht, kleiner oder gleich als ein bestimmten Wert zu kommen, spiegelt sich die Grafik einfach.
Für einen kleineren Würfel wie den W6 wird sie gestaucht, für einen größeren wie dem W20 gestreckt. Die Form der Wahrscheinlichkeitsverteilung ändert sich nicht, nur die Schrittweite ist bei den verschiedenen Würfeln unterschiedlich. Die Grafik zeigt als Beispiel den W6.

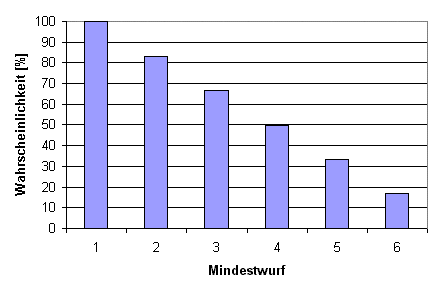
2) Mehrere Würfel

Eine andere Möglichkeit für eine Probe ist es, mehrere gleiche Würfel zu nehmen und dann zu schauen, ob mindestens einer den Mindestwurf geschaft haben. Die Berechnung der Wahrscheinlichkeiten hierfür will ich an einem Beispiel erklären. Soviel vorweg: Wer meint, die Wahrscheinlichkeit verdoppelt sich einfach, der irrt. Mit etwas Überlegung wird klar, das dies auch gar nicht möglich ist, denn dann wäre die Wahrscheinlichkeit bei 1 ja 200%.
Wir nehmen also mal zwei W10. Die Wahrscheinlichkeit für einen Mindestwurf von 5 ist 60% für den ersten Würfel (siehe oben). Sie ist auch wieder 60% für den zweiten Würfel. Dieser ist aber nur dann von Interesse, wenn der erste nicht erfolgreich war, also in 100% minus 60% macht 40% der Fälle. Daher multiplizieren sich die 40% der Fälle mit den 60% Wahrscheinlichkeit, dass der Würfel ein Erfolg ist: 40% mal 60% ergibt 24%, dass der zweite Würfel zum Erfolg der Probe führt. Diese kommen zu den 60% des ersten Würfels hinzu, wodurch sich für die beiden Würfel zusammen eine Wahrscheinlichkeit von 84% ergibt. In der Grafik sieht das dann wie folgend aus:

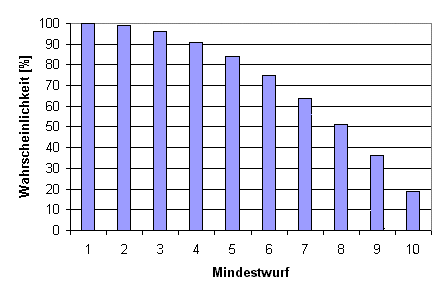
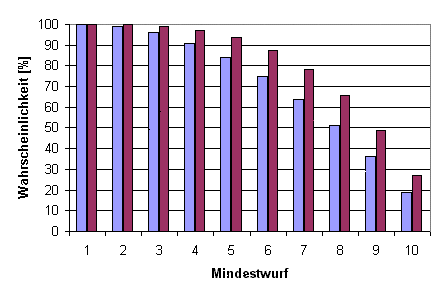
Wie man erkennt, handelt es sich nun nicht mehr um eine gleichmäßige Abnahme der Wahrscheinlichkeit, sondern um ein erst langsames, dann immer schneller werdendes Fallen. Wenn wir nun noch einen dritten W10 hinzunehmen, bietet auch er zuätzliche 60% Wahrscheinlichkeit für einen Erfolg in dem Bereich der 16% (100%-84%) des bisherigen Mißerfolges. Alle drei Würfel zusammen kommen dann also auf 84% plus 16% mal 60%, das ergibt 93,6%. Die Grafik zeigt, wie der Verlauf bei 3W10 (rot) im Vergleich zu den 2W10 (lila) noch gebogener wird:

3) Addierte Würfel

Anstatt die mehreren Würfel einzeln gegen den Mindestwurf auszuwerten, kann man auch die gewürfelten Zahlen addieren und dann die Summe mit dem Mindestwurf vergleichen. Hieraus ergibt sich wiederrum ein anderer Verlauf der Wahrscheinlichkeitsverteilung.
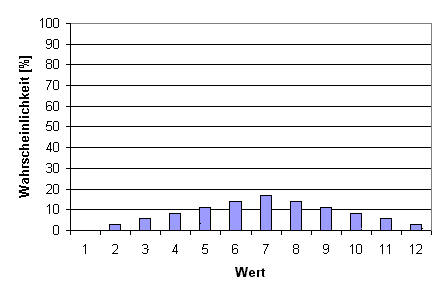
Kommen wir zunächst erstmal wieder zu den Wahrscheinlichkeiten der einzelnen Werte. Bei diesem System ist die Wahrscheinlichkeit bei dem Durchschnitt der Zahlenwerte am höchsten. Er berechnet sich als kleinster möglicher Wert plus größtem möglichen Wert und dann das Ergebnis halbiert. Für zwei addierte W6 kommt man also auf 2 (zwei Einsen gewürfelt) plus 12 (zwei Sechsen gewürfelt) durch 2, also 7. Diese Wahrscheinlichkeitsveteilung ergibt sich dadurch, dass es für die Summen der beiden Würfel verschieden viele Kombinationsmöglichkeiten gibt: Um eine Summe von 2 zu bekommen, müssen beide Würfel eine Eins zeigen, das ist nur eine Möglichkeit. Für eine 3, kann der erste Würfel eine Zwei sein, der andere eine Eins, oder aber der erste eine Eins und der andere eine Zwei, das ergibt zwei Möglichkeiten. Die Wahrscheinlichkeit für die einzelnen Summen ändern sich bei zwei addierten Würfel linear, da immer eine zusätzliche Möglichkeit den Wert zu erreichen hinzukommt. In der Grafik sieht man daher eine dachartige Verteilung mit einem Höhepunkt über dem Durchschnitt. Hier wird dies für 2 addierten W6 gezeigt.

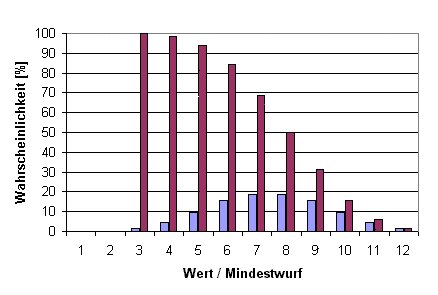
Geht es nun wieder darum über einen bestimmten Mindestwurf zu kommen, so addieren sich genau wie bei einem Würfel die Moglichkeiten. Da es für mittleren Zahlen (6,7,8) mehr Kombinationen gibt als für die Äußeren (2,3 oder 11,12) verläuft die resultierende Kurve dort steiler und an den Enden flacher:

Wenn man mehr als zwei Würfel addiert, nimmt die Kurve der Wahrscheinlichkeit der Würfelwerte eine Glockenform an (lila). Entsprechend ausgeprägter werden damit auch die flach auslaufenden Enden und die steile Mitte bei Würfen gegen einen Mindestwurf (rot). Hier gezeigt an drei addierten W4, die genauso wie zwei W6 auf einen maximalen Wert von 12 kommen können.

Auswirkungen auf das Rollenspiel

Was aber bedeuten diese Wahrscheinlichkeitsverteilungen nun für das Rollenspiel? Welches System hat wo Vorteile und welche Nachteile. Grundsätzlich muss erstmal festgehalten werden, dass es kein Würfelsystem gibt, das für jedes Rollenspiel optimal wäre. Je nach der Stimmung des Spiels, den verwendeten Fertigkeiten und ausgewürfelten Situationen, kann mal das eine mal das andere System besser sein.

Eine wichtige Frage an das Würfelsystem ist, wie sich die Wahrscheinlichkeiten mit steigendem Mindestwurf ändern. Wird mit nur einem Würfel zum Beispiel dem W20 aber auch dem W% gearbeitet, so haben wir es mit einer linearen Wahrscheinlichkeitsänderung zu tun (siehe 1).

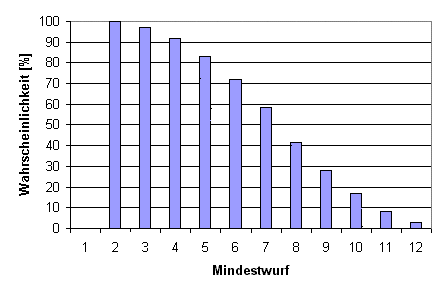
Im Vergleich dazu haben zwei addierte Würfel eine Kurvenform, welche die Extremwerte seltener werden läßt (siehe 3). Dies hat den Vorteil, dass einfache Proben mit einer größeren Sicherheit gemeistert werden und es gleichzeitig sehr schwere Mindestwürfe geben kann, die nur selten geschafft werden. Gibt es in dem Würfelsystem eine Regel, die den best- und schlechtmöglichsten Würfelwert als kritischen Erfolg bzw. Patzer auslegt, so reduziert sich auch für diese beiden Ereignisse die Häufigkeit ihres Auftretens.
Die addierten Würfel bieten dafür einen steileren Verlauf im mittleren Bereich, sodass sich zwei mittlere Mindestwürfe in ihrer Schwierigkeit stärker unterscheiden als bei einem Würfel, was bei zu kleinen Würfeln (vor allem dem W4) zu einer sehr geringen Differenzierung der Mindestwürfe und damit der Schwierigkeiten führt.

Das System mit mehreren Würfeln einzeln gegen den Mindestwurf (siehe 2) vermeidet auch Misserfolge bei geringen Mindestwurf, erhöht aber dabei die Wahrscheinlichkeit für besonders gute Ergebnisse. Damit eignet es sich weniger für besonderen Realismus als vielmehr für Superhelden.
Als Bonus dieses Systemes erhält man automatisch und ohne Rechnen sofort eine Aussage darüber, wie gut die Probe gelungen ist, indem man die Anzahl der erfolgreichen Würfel bestimmt. Dies bietet vor allem für die Bestimmung des Schadens im Kampf gute Möglichkeiten.

Exoten

Mit den hier vorgestellten 3 grundlegenden Verfahren sind noch lange nicht alle Rollenspiele abgedeckt. Erwähnt sei hier nur Shadowrun, das mit mehreren W6 arbeitet und durch erneutes Würfeln der erfolgreichen Würfel auch noch schwer zu erreichende Mindestwürfe über dem normalen Bereich einführt. Dadurch entsteht aber eine sehr komische Wahrscheinlichkeitsverteilung: So halbiert sich die Wahrscheinlichkeit bei Erhöhung des Mindestwurfes von 5 auf 6, ändert sich auf 7 aber gar nicht! Da aber z.B. ein Laserpointer an der Waffe immer einen -1 bietet, hat er mal starke Auswirkungen, mal keine.

Weitere Aspekte

Mit der Betrachtung der Würfel ist ein System noch lange nicht komplett durchdacht. Es stellt sich vor allem die Frage, wie Mindestwürfe ermittelt werden: Wird er aus Schwierigkeit und Fertigkeit berechnet? Kommt noch ein Attribut hinzu? Beeinflusst der Fertigkeitswert die Art oder Anzahl der Würfel?
Je mehr gerechnet und nachgeschaut werden muss, desto langsamer wird das System, was das eigentliche Rollenspiel behindern kann. Also heisst es nicht nur nach dem optimalen Realismus und Detailreichtum gucken, sondern einen Kompromiss mit der Spielgeschwindigkeit eingehen. Darin liegt die Kunst eines guten Würfelsystems.